Media, Moda, Mediana
Classificazioni
Classificare significa mettere insieme elementi che hanno una determinata caratteristica. Gli elementi che si prendono in considerazione si dice che fanno parte di un UNIVERSO.
Allora prendiamo ad esempio l’Universo numeri a una cifra così rappresentato
vediamo che alcuni sono scritti in nero, altri in rosso. Procediamo.
Per rappresentare le classificazioni esistono diversi tipi di diagrammi:
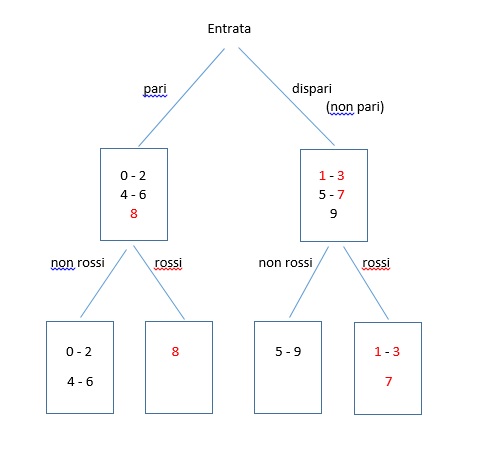
diagramma ad albero
L’entrata rappresenta tutti gli elementi considerati,
poi li ho raggruppati suddividendoli in pari e dispari (non pari), nell’ordine possono essere anche chiamati A e NON A.
Ho continuato la classificazione separando in ogni primo raggruppamento – A e NON A – i rossi e non rossi, nell’ordine B e NON B.
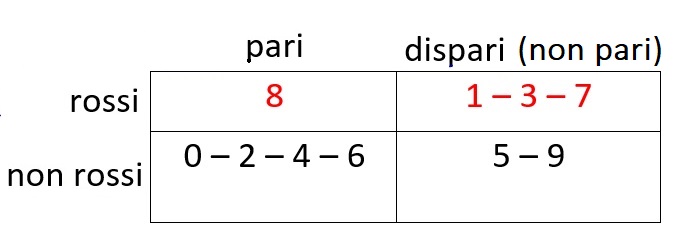
Diagramma di Carroll
La stessa suddivisione la posso rappresentare con un altro tipo di diagramma, cambia la grafica (il disegno), ma i raggruppamenti saranno sempre gli stessi. Si può leggere facilmente evidenziando tutti gli elementi con una caratteristica, ad esempio pari (A), oppure con due caratteristiche, e quindi pari e non rossi (A, NON B).
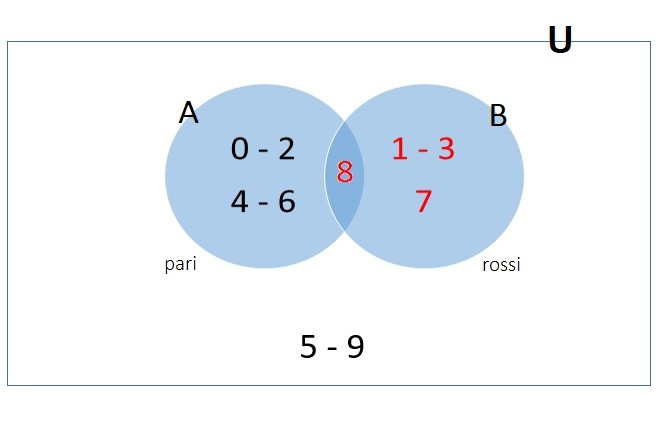
Diagramma di Venn
L’ultimo diagramma che presento è quello nel quale si fa graficamente ricorso all’utilizzo degli insiemi, ma il risultato è sempre lo stesso. Qui vediamo evidenziato l’Universo U e all’interno i due insiemi pari (A) e rossi (B), c’è quindi un punto in cui i due insiemi coincidono, si chiama intersezione, è il punto in cui ci sono gli elementi con entrambe le caratteristiche evidenziate in ciascun insieme (nel nostro caso pari e rossi), tutti gli altri elementi che non posseggono le caratteristiche evidenziate (elementi NON A e NON B) restano al di fuori dei due insiemi, ma comunque nell’Universo U.
torna a Matematica